Best Of The Best Tips About How To Tell If An Integral Is Improper

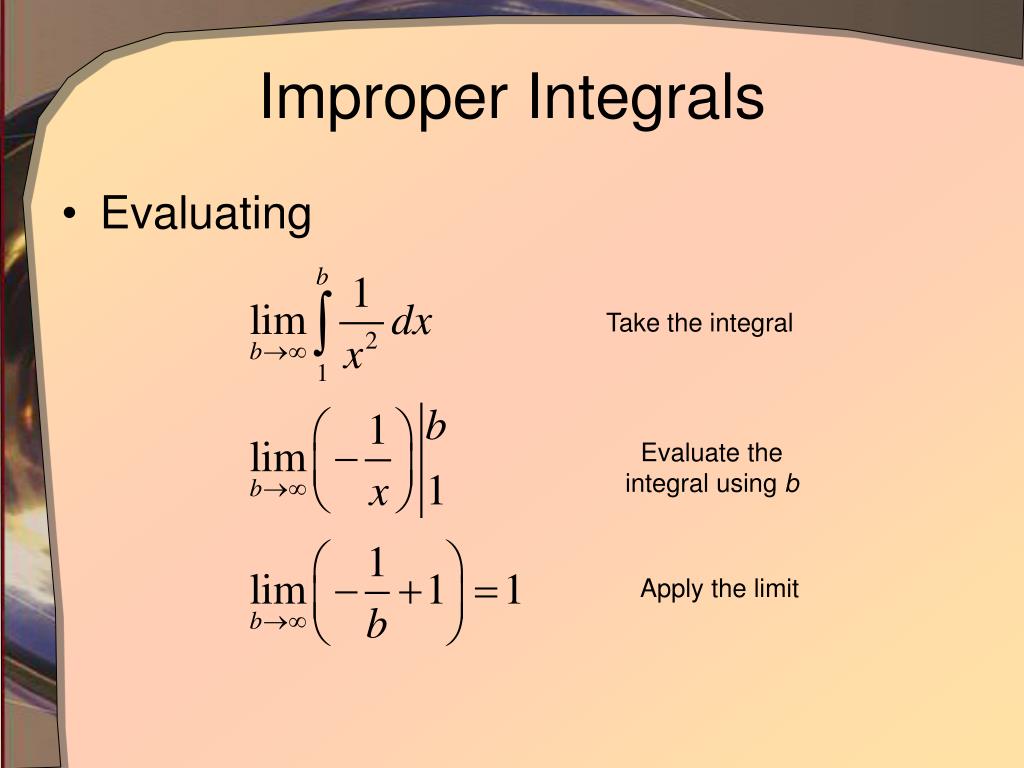
Recall that the first step in analyzing any improper integral is to write it as a sum of integrals each of has only a single “source of impropriety” — either a domain of integration that extends to \(+\infty\text{,}\) or a domain of integration that extends to \(.

How to tell if an integral is improper. When you integrate, you are technically evaluating using rectangles with an equal base length (which is very similar to using riemann sums ). You’re taking a known length (for. Both of these are examples of integrals that are.

Type in any integral to get the solution, free steps and graph Remember that a definite integral is an. Asked 7 years, 11 months ago.

The function f(x) was continuous on [a, b] (ensuring that the range of f was finite). The limit does not exist or it is infinite, then we say that the improper. 8.7k views 3 years ago larson calculus 8.8.

Improper integrals are definite integrals where one or both of the boundaries is at infinity, or where the integrand has a vertical asymptote in the interval of integration. How to determine if an integral is an improper integral. In each case, if the limit.

Since they are defined, then this is not a type i. 1.4integration formulas and the net change theorem. Identify whether one or both of the bounds is infinite.

Improper integrals are definite integrals that cover an unbounded area. The interval over which we integrated, [a, b], was a finite interval, and. In this section we need to take a look at a couple of different kinds of integrals.

The limit exists (and is a number), in this case we say that the improper integral is convergent ; Section 7.8 : F ( x) be continuous over an interval of the form.

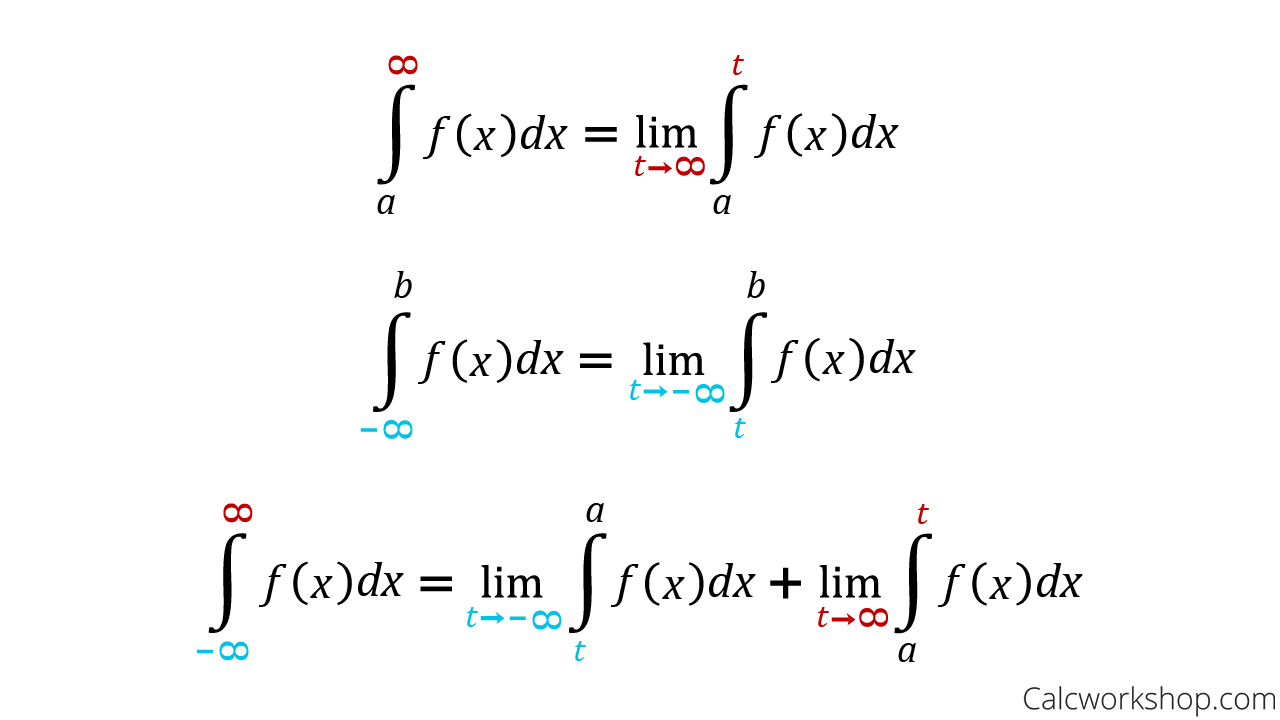
1.3the fundamental theorem of calculus. ( − ∞, b] then. Improper integrals are just like definite integrals, except that the lower and/or upper limit of integration is infinite.

Simple improper integrals are de ned to be the appropriate limits of proper integrals, e.g.: For each of the following definite integrals, decide whether the integral is improper or not. Note that our respective upper and lower bounds are 1 and 2.

1 1 x dx { if the limit exists as a real number, then the simple. If the integral is proper, evaluate it using the first ftc.